Ma première carte mentale !
ven. 21 août 2020
Catégorie : Préparations de cours
Tags : Préparation Progression SupportsPédagogiques Vacances
Le mois d'août est bien avancé, la rentrée approche. Et quelle rentrée ! L'épidémie de Covid-19 rend les choses éminemment difficiles à anticiper. Mais ce n'est pas l'objet de cet article.
Malgré les incertitudes, j'ai pris le parti de préparer mes séquences et mes séances comme d'habitude, en faisant les aménagements qu'il faut au fur et à mesure, selon l'évolution de la situation. Donc, je prépare mes cours. Il n'est évidemment pas question de tout reprendre à partir de rien : sans en avoir l'air, j'entame ma quatrième année en tant que prof. Je commence à avoir un ensemble d'activités et d'exercices que j'aime bien et que je garde d'une année sur l'autre. Ce qui n'empêche pas d'apporter des changements, parfois importants, lorsque certaines choses que j'ai faites les années passées ne m'ont pas plu. Et de fait, j'ai déjà commencé à reprendre mes cours depuis déjà deux semaines, à raison de 4 à 6 h par jour (quand même !).
Voici un exemple de support que je vais changer cette année, au niveau 5e.
Les angles en 5e
Au programme de l'année de cinquième, on trouve les angles. Plus précisément, il est attendu des élèves qu'ils sachent, en fin d'année :
- nommer et mesurer correctement des angles avec le rapporteur ;
- calculer des mesures d'angles dans un triangle ;
- reconnaître les angles aigus, obtus, droits, plats ainsi que les angles complémentaires et supplémentaires ;
- utiliser les angles alternes-internes et correspondants à bon escient.
Naturellement, il n'est pas question de tout faire en une seule séquence, cela ferait trop. Pour la séquence qui nous intéresse, je vais aborder les items 1 et 4.
La séquence suit un déroulé tout à fait classique : activité d'introduction sur les angles alternes-internes, cours, exercices. Je ne prévois pas d'activité spécifique pour nommer les angles, nous l'aborderons plutôt de manière perlée pendant toute la séquence, et notamment pendant les questions flash.
Et donc, la nouveauté ?
Comment c'était avant
J'ai déjà fait une séquence très similaire l'année dernière au niveau 5e, j'ai donc repris beaucoup de choses à l'identique, car cela avait bien fonctionné. Enfin, sauf la partie cours (la « trace écrite » si on veut faire du jargon). Il y avait beaucoup de vocabulaire, donc beaucoup de texte ; et finalement, c'était verbeux et pas tellement clair.
En feuilletant des manuels, j'ai vu qu'à la fin de certaines séquences, des cartes mentales sont proposées. J'ai toujours été assez frileux avec ce genre de supports, mais plusieurs de mes collègues (en histoire-géographie, notamment) les utilisent beaucoup et les retours des élèves sont plutôt positifs.
Puisque la leçon que je proposais sur les angles ne me plaît pas trop, c'est peut-être l'occasion de tester autre chose… Donc je me lance ! Pas question de changer le contenu, seulement la forme. Je reprends donc le cours, et je sors un papier de brouillon pour essayer de synthétiser et de regarder plus en détails les liens entre les sections. Le plan du cours est le suivant :
- Vocabulaire
- Nommer les angles
- Angles aigus, angles obtus
- Angles alternes-internes, angles correspondants
- Droites parallèles, droites sécantes
- Angles correspondants et droites parallèles
- Angles alternes-internes et droites parallèles
Avec un examen un peu attentif de ce plan, on voit tout de suite que les idées ne sont pas très bien reliées entre elles, et que les connexions logiques entre les sections ne sont pas faciles à voir.
Comment ça va être cette année
Je vais donc proposer aux élèves une présentation totalement différente de la trace écrite, qui prendra la forme d'une carte mentale distribuée. La voici en exclusivité :
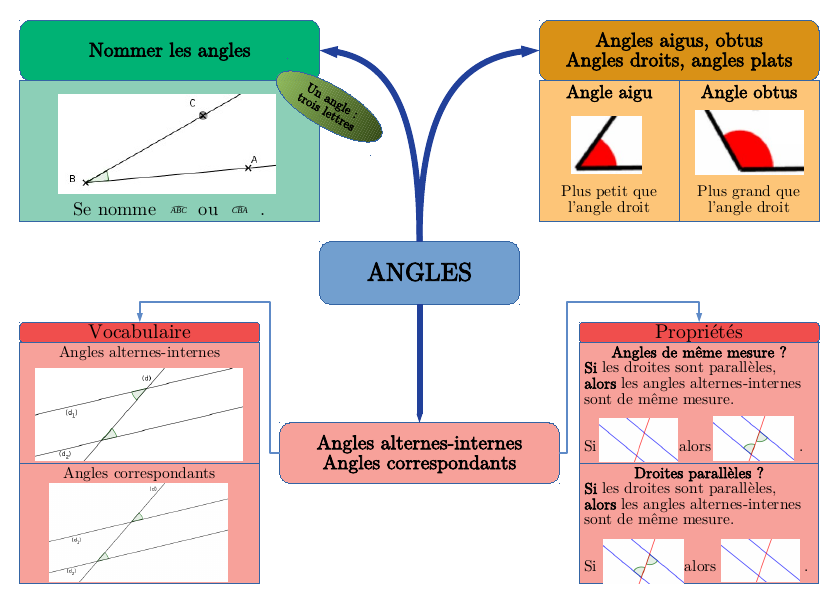
Carte mentale pour la trace écrite de la séquence « Les angles (1) »
Voilà, j'espère que c'est lisible et suffisamment clair. C'est en tout cas très synthétique et résume l'essentiel. J'imprimerai en grand le document pour le laisser collé au mur dans ma salle, et les élèves en auront un exemplaire papier à conserver, qui tiendra lieu de cours.
Bémol : en temps normal, j'écris le cours au tableau et les élèves doivent le recopier. J'y tiens beaucoup, c'est à mon avis une étape importante pour comprendre et mémoriser, d'autant plus que cette phase d'écriture me permet souvent de canaliser la classe et d'identifier les points qui n'ont pas été compris.
Il faut donc que je trouve une alternative à la recopie, puisque la carte sera distribuée. Et là encore, je vais m'inspirer de ce que font les collègues (je les en remercie, même s'ils ne le savent pas :D ) : je vais distribuer la carte mentale vide avec simplement les items à remplir, un peu comme on pourrait donner un fond de carte à compléter en géographie :
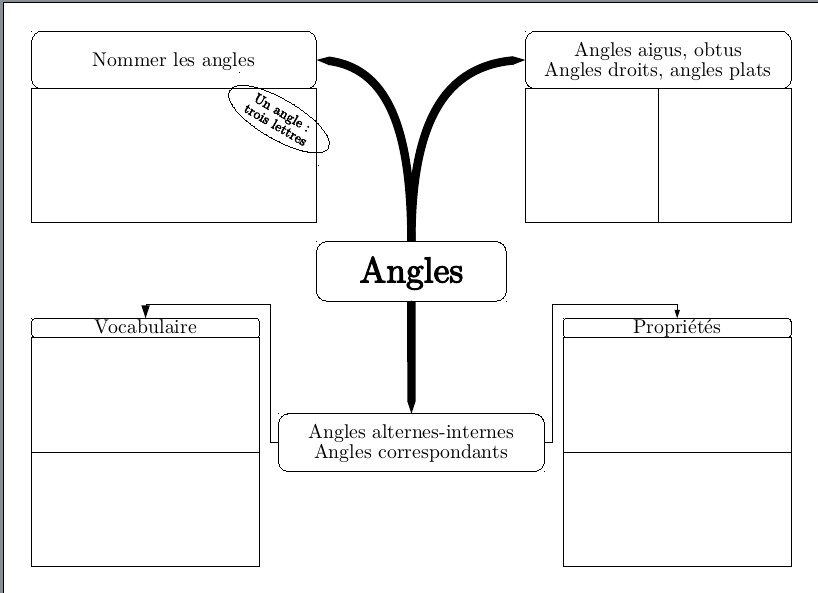
Carte mentale vide, à compléter
Je vais également donner des petites cartes, avec tous les éléments possibles, dissociés les uns des autres. Et ça sera aux élèves de les assembler afin qu'ils construisent la carte :
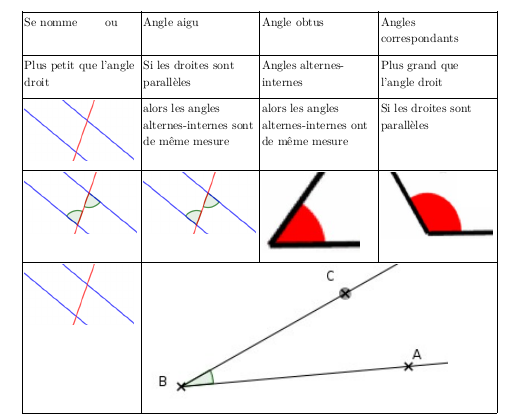
Les éléments de la carte mentale, à assembler convenablement
Pfiouuu !
Voilà l'idée générale. Je sors très largement de ma zone de confort, ce n'est pas du tout un support auquel je suis habitué, donc j'ai hâte de voir ce que cela va donner.
Mine de rien, cela m'a pris plusieurs heures pour en arriver à cela ; sans doute parce que c'est très nouveau pour moi, donc j'ai dû lire des ressources, réfléchir beaucoup. La séquence aura lieu normalement un peu avant les vacances de la Toussaint ; nous verrons à ce moment-là ce que ça va donner.
Chroniques d'un prof de maths — Propulsé par Pelican et Bootstrap — Icônes par Font Awesome et Font Awesome More
Tous les articles sont publiés sous licence Creative Commons BY.
