Une nouveauté en calcul littéral
Quelle semaine ! C'est reparti après la période janvier-mars qui a été très dense, notamment avec la semaine des mathématiques et le grand jeu organisé pour la visite de CM2. J'aurais aimé rédiger un article sur le bilan de cet escape game incroyable, mais je n'ai pas eu le temps. En résumé, c'était un très bon moment, dans une période difficile pour l'établissement. Une demi-journée de synergie exceptionelle entre les adultes et les élèves. Et franchement, les dizaines d'heures de travail passées valaient le coup !
Mais ça, c'était il y a plus de deux mois. Maintenant, c'est la première semaine après les vacances, et ça commence fort :
- brevet blanc pour les 3e jeudi (12 mai) et hier (13 mai), avec à la clé pour les profs des copies à corriger.
- on attaque une nouvelle séquence avec les 5e, sur les nombres entiers. Avec une façon de faire de la différenciation que je n'avais jamais testée jusqu'à maintenant. Ça s'est très bien passé pour le moment, j'ai hâte de voir comment ça va continuer et je ferai peut-être un article spécifique si j'ai le temps.
- j'ai été confronté à la gestion d'un incident étrange avec des élèves de 5e dont je suis le professeur principal. Certaines et certains d'entre eux ont apporté des œufs afin, disent-ils, de faire un gâteau pour une élève dont c'est l'anniversaire. Sauf qu'au hasard d'une situation de classe en cours de français, cette histoire d'œufs est venue à nos oreilles et nous n'avons pas encore tout démêlés. Nous sommes très attentifs et attentives à cela car il y a eu plusieurs histoires d'enfarinage des jours d'anniversaire… À suivre.
- un magasin coopératif dont je suis membre, Coquelicoop, prépare la clôture de ses comptes et s'engage dans une profonde réflexion stratégique pour le 2e semestre 2022 et l'année 2023. Étant très investi dans le fonctionnement de la coopérative, cela m'occupe pas mal.
- enfin, et c'est l'objet de cet article, on a attaqué la distributivité double avec les classes de 3e. Mais pas comme d'habitude.
De quoi parle-t-on ?
La distributivité double est le nom que l'on donne usuellement à la propriété suivante : « Soient a, b, c, d quatre nombres. Alors, (a+b)(c+d)=ac+ad+bc+bd). »
D'habitude, j'introduis cette propriété de deux façons différentes.
D'abord, comme une généralisation de la propriété de distributivité simple, qui s'énonce comme suit : « Soient k, a et b trois nombres. Alors, k(a+b)=ka+kb. » Puis on développe et on pose k=(c+d). Mais cela reste assez difficile à comprendre pour les élèves.
Une autre façon, plus géométrique, consiste à considérer un rectangle coupé en deux dans le sens de la longueur et en deux dans le sens de la largeur. On obtient ainsi quatre rectangles, de longueurs respectives a et b et de largeurs c et d. Et l'aire du grand rectangle est (a+b)(c+d) (longueur×largeur), mais aussi ac+ad+bc+bd (somme des aires des quatre rectangles).
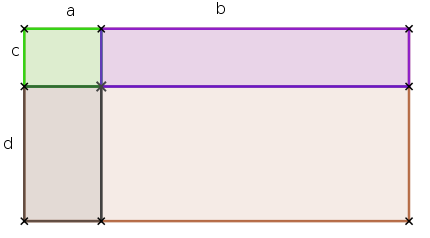
Distributivité double avec un rectangle
Vous trouvez ça lourd et verbeux ? Moi aussi. J'ai donc essayé de trouver autre chose
Une idée originale (enfin, je crois)
En feuilletant un manuel, je trouve cet exercice :

Exercice 43 page 80, Mission Indigo, 3e, 2016
Je le trouve intéressant, et je me dis que cela pourrait même être exploité en introduction, en se basant sur… la multiplication posée des nombres entiers ! Mais je ne trouve aucune source pour ça, donc c'est parti ! Je fais ce que (presque) tous les profs adorent dans le métier : j'invente.
Je vous raconte comment ça se passe dans ma tête.
Papier de brouillon !
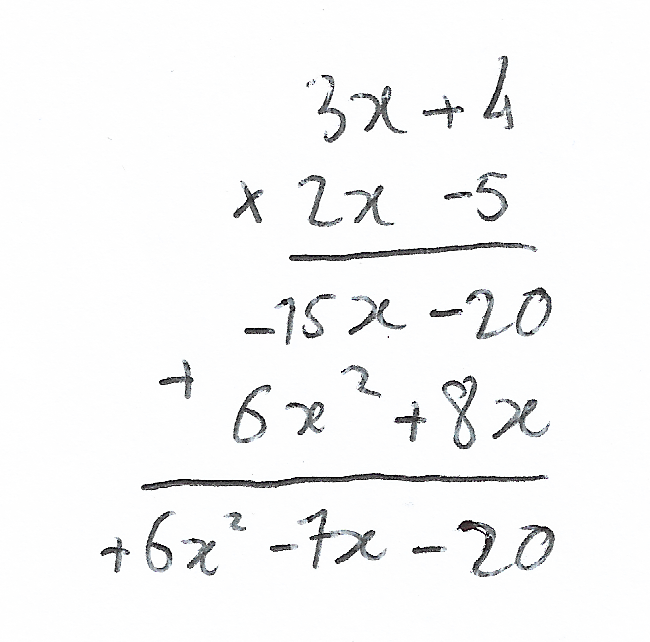
Brouillon - Étape 1
Je reprends l'énoncé de l'exercice, et je pose (3x+4)×(2x-5).
OK c'est pas mal, mais pour les élèves il y a un truc qui cloche. Déjà, il faudrait davantage d'étapes de calcul. Mais à ce stade ce n'est pas grave : c'est le brouillon du prof, on pourra ajouter les étapes plus tard.
Plus problématique : les termes constants, les termes en x et les termes en x² ne sont pas alignés les uns sous les autres. Il faudrait appliquer un décalage vers la gauche pour la deuxième ligne. Qu'à cela ne tienne !
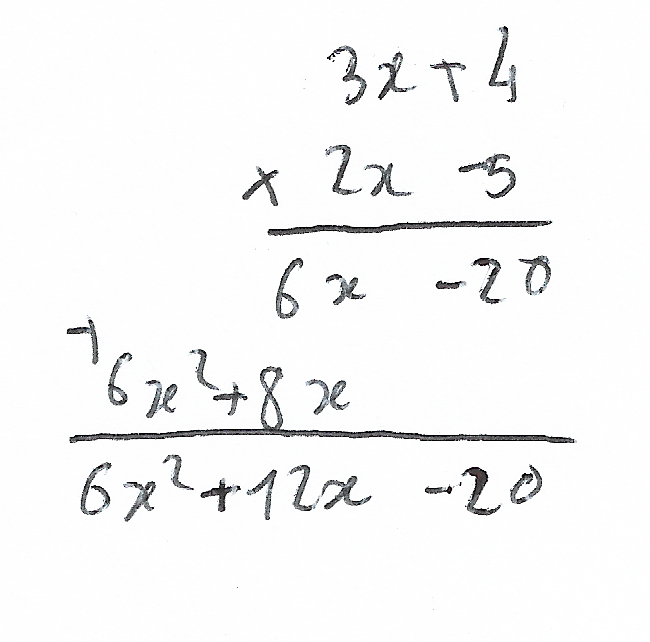
Brouillon — Étape 2
C'est un peu mieux. Mais comment justifier aux élèves ce décalage ? Dire qu'on décale parce que c'est « pratique » ? Bof, j'aimerais mieux une justification mathématique.
Pourquoi effectue-t-on ce décalage, en réalité ? Pour des raisons d'homogénéité : on additionne ensemble les mêmes puissantes de x. Et finalement, c'est comme pour les multiplications de nombres entiers à deux chiffres : on « ajoute un zéro » (comme disent les élèves), et en réalité on décale d'un rang vers la gauche, pour aligner unités avec unités, dizaines avec dizaines, centaines avec centaines.
Voilà l'analogie qu'il me faut : x joue en fait le rôle de la puissance de 10 dans la décomposition décimale. Ça y est, je sais comment faire !
L'idée qui change tout ?
Si l'on pose 34×15, c'est comme ça :
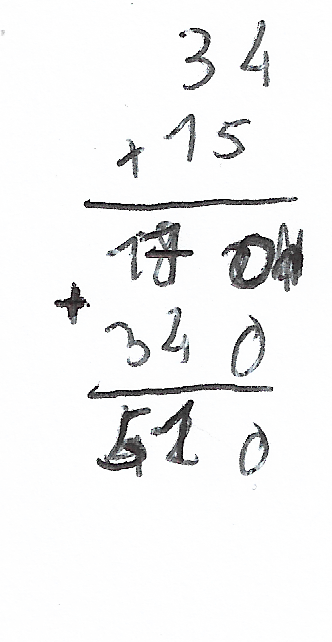
Brouillon — Étape 3
(C'est un brouillon, il y a des ratures : quoi de plus normal ? :) )
Et si on veut poser, plus étrange, (30+4)×(20-5) ?
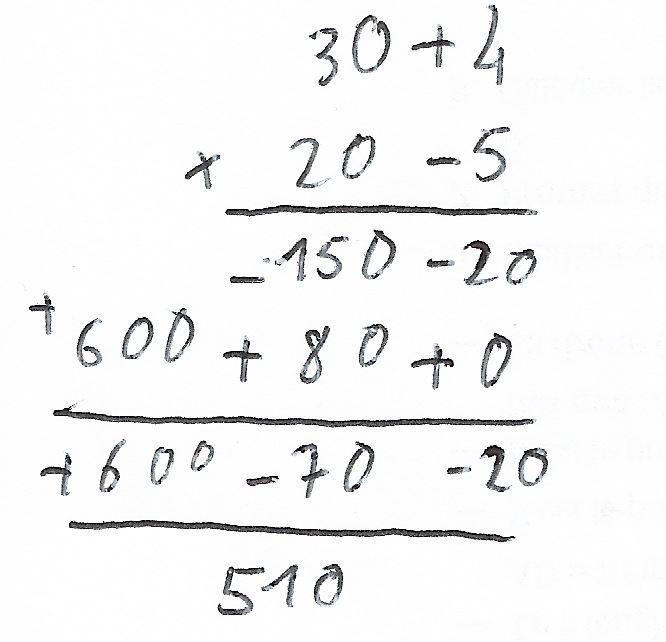
Brouillon — Étape 5
C'est quand même très élégant. Et cela s'adapte très bien à (3x+4)×(2x-5). Mais en fait, il faudrait même faire apparaître le 2x×0 explicitement :
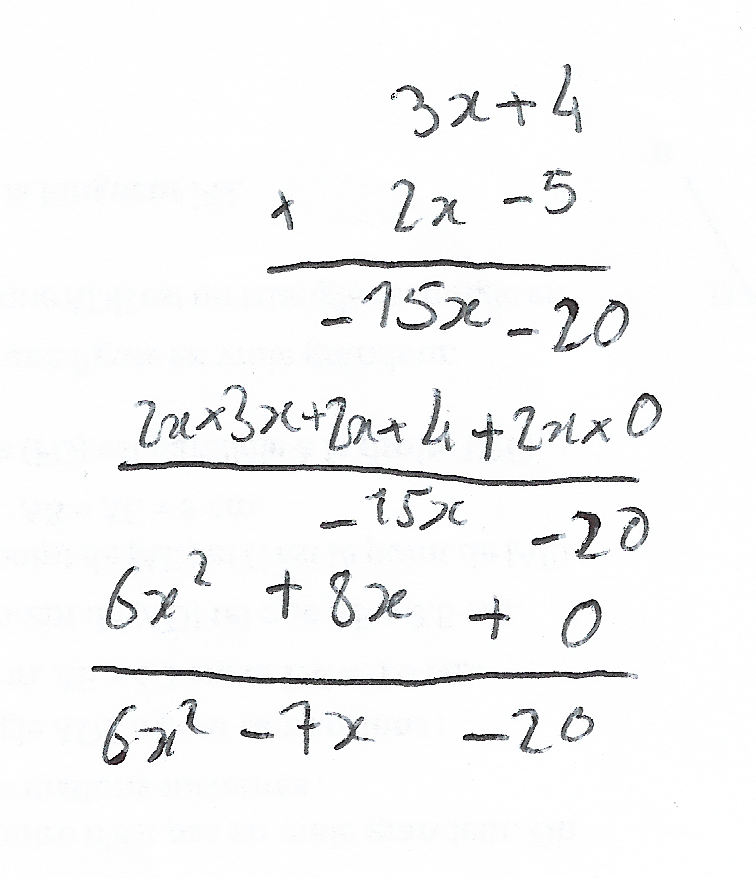
Brouillon — Étape 6
Vers l'activité finale
Mine de rien, j'ai réfléchi une bonne demi-heure. Et les figures que vous voyez sont propres et bien ordonnées, rien à voir avec le vrai brouillon. J'aurais bien aimé le montrer, mais impossible de le retrouver, je l'ai probablement jeté… C'est inévitable : les brouillons sont des œuvres éphémères. :P
Document donné aux élèves
En fin de compte, je n'aime pas trop l'exemple avec l'expression (3x+4)×(2x-5). Je change et je remplace par (2x+3)(4x-2). Je distribue donc cet énoncé :

Énoncé distribué aux élèves
Leur première réaction, face à la question 1)a) a été : « Bah c'est logique, il faut faire quoi ? » Et ils ont eu raison, une formulation du type « Commençons par observer que… », sans poser la question eût été préférable. J'en prends note pour les prochaines fois.
Ensuite, au 1)b), c'était moins évident. Pas surprenant, car on ne pose jamais (20+3)×(40-2) de cette façon. J'avais anticipé le blocage, donc j'avais préparé un exemple avec des valeurs différentes :
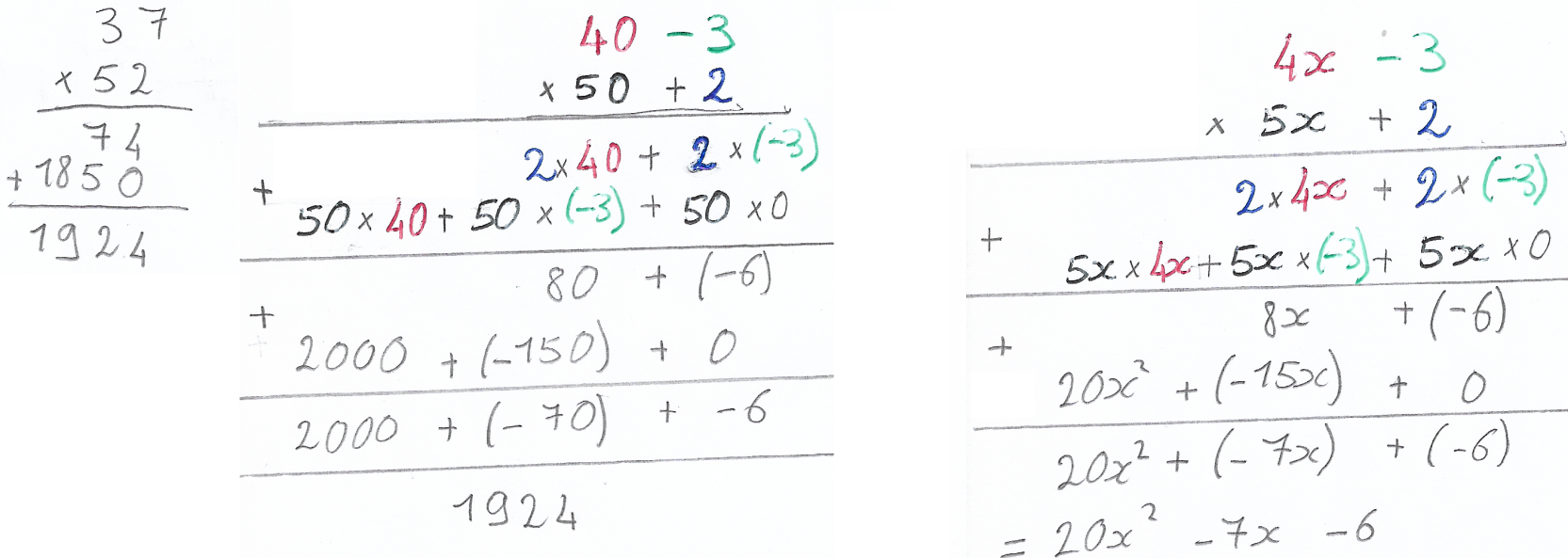
Exemple projeté au tableau
J'avais totalement écrit l'exemple en avance et je l'ai projeté au tableau, car je souhaitais que les élèves voient immédiatement le résultat final, sans me voir effectuer les calculs en direct. Car cela aurait été un peu fastidieux avec les couleurs. Et aussi pour limiter au maximum le temps d'écoute passive. Je préfère une lecture et une réflexion actives s'appuyant sur un document abouti (mais rudimentaire, certes).
Quelques remarques
Vous pouvez observer que par rapport aux brouillons que j'ai montrés plus haut, il y a beaucoup de changements ! Et en premier lieu évidemment, les couleurs. Les étapes du calcul, également, sont plus détaillées.
On a bien mis 50×0 pour la multiplication et ici, le 5x joue le rôle des dizaines. Comme si x pouvait être substitué par 10. D'ailleurs, remarquez que que dans la colonne des centaines, on voit apparaître x². C'est cohérent.
Pendant la séance
L'exemple ci-dessous était projeté au tableau et j'ai demandé aux élèves de l'examiner attentivement et de s'en inspirer pour (2x+3)(4x-2).
Très rapidement apparaît la question : « Pourquoi vous avez mis 5x×0 ? ». Question fort légitime, et c'est là que l'analogie opère ! On s'inspire très fortement de la multiplication des nombres entiers.
Bien sûr, les élèves m'ont fait remarquer que poser (40-3)×(50+2) est beaucoup plus long que 37×52, ce qui est vrai. À cette remarque, j'ai simplement répondu qu'ils avaient raison, mais que cela nous serait utile à titre d'étape intermédiaire pour s'inspirer du modèle en calcul littéral.
C'est un raisonnement par analogie, très utile en mathématiques.
Je laisse aux élèves 10 bonnes minutes pour analyser l'exemple et je circule dans les rangs pour débloquer les erreurs de signe, les incompréhensions sur les alignements des nombres ou des lettres, etc.
Puis, après 10 minutes supplémentaires, plus de 80% des élèves ont réussi à répondre à la question b). C'est vraiment bien car rarement sur ce chapitre, les élèves n'ont autant d'aisance sur la distributivité double.
Et après ?
La suite de la séquence est consacrée au cours, beaucoup plus classique, et à des exercices, classiques également.
Il y a quand même beaucoup de choses à tirer de cette activité, sur le plan mathématique.
- Déjà, il est intéressant de remarquer qu'en fait, chaque ligne du calcul posé est en fait une application de la distributivité simple ! Ainsi, (4x-3)×2 = 2×4x + 2×(-3) et (4x-3)×5x = 20x²-15x.
- On travaille énormément de compétences différentes ! Représenter, évidemment puisque nous exprimons le même calcul de plein de façons différentes. Mais aussi calculer et surtout raisonner.
- Pourtant, il n'y a aucune démonstration ici, uniquement des jolis raisonnements élémentaires et des analogies bien pesées pour donner l'intuition (clin d'œil au génial livre Mathematica, une aventure au cœur de nous-mêmes de David Bassis, qui réhabilite l'intuition en mathématiques) des choses.
Au bilan, je suis vraiment très content de cette activité ! C'est bien la première fois que des élèves me disent que « la distributivité, c'est facile en fait ! ». Et d'ailleurs, beaucoup mon demandé s'ils « ont le droit » de poser de cette façon « en contrôle ou au brevet ».
Et ma foi, pourquoi pas ? C'est joli, propre et riche sur le plan mathématique. Mais c'est quand même assez atypique, donc attention à ne pas s'enfermer dans des méthodes trop originales. C'est fort dommage, mais les programmes laissent peu de place à la liberté et à la construction des intuitions.
Il reste à travailler les automatismes pour intérioriser la méthode et gagner en souplesse sur la technique. Mais en fait, cette façon d'aborder le sujet, intimidante à première vue, me paraît limpide et a même éclairé ma propre compréhension de certains enjeux didactiques en calcul littéral.
L'année prochaine, je ferai peut-être la distributivité simple aussi de cette façon. Je suis réellement convaincu que c'est une bonne façon de faire.
Chroniques d'un prof de maths — Propulsé par Pelican et Bootstrap — Icônes par Font Awesome et Font Awesome More
Tous les articles sont publiés sous licence Creative Commons BY.
