Jeudi 29/06, 22h15, retour de Conseil d'Administration au collège après avoir passé la matinée à corriger le brevet. Plus l'actualité brûlante, avec un policier qui exécute un adolescent dans le cadre d'un contrôle routier, la journée a été longue.
Quoi de mieux que faire, inopinément, des maths pour se changer les idées ?
L'occasion d'illustrer un mail reçue par ma cheffe d'établissement un soir, alors qu'il ne m'était pas destiné, auquel elle a répondu avec humour le lendemain : « Comme quoi; il ne faut rien faire passé 20 h 30 ».
Petit exercice de géométrie
En flânant sur Internet et sur les réseaux sociaux hier soir, je tombe sur une publication d'Image des Maths, relayée par un collègue :
Si le côté vertical du rectangle mesure 1 cm, combien mesure son côté horizontal ?
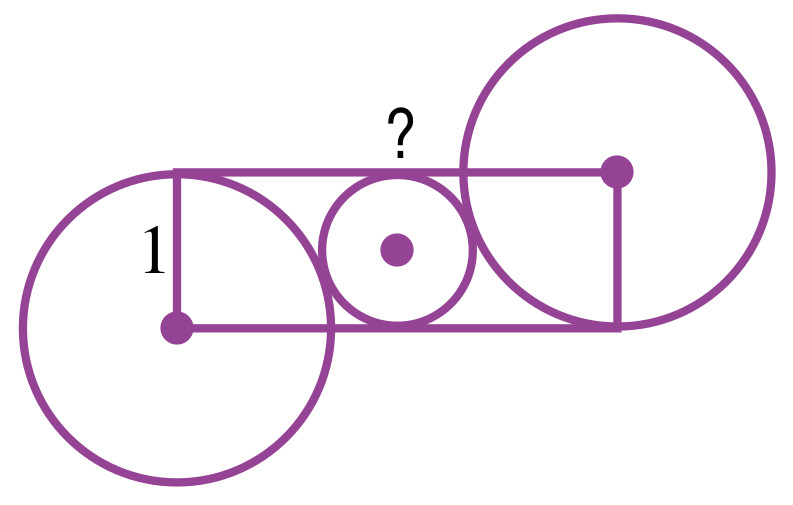
En effet, c'est sympa et le collègue qui relaye la publication indique : « Un joli problème ouvert de géométrie accessible dès la 4ème, pour ce qui est des connaissances. De l'intérêt de bien coder la figure. »
Il est tard, mais ça m'intrigue. Je cherche un peu, mais clairement je suis fatigué. Bon, on note ABCD le rectangle, O le centre du petit cercle et x la longueur inconnue.
Puis j'applique le théorème de Pythagore dans divers triangles, j'arrive à écrire des choses. Mais visiblement, je tourne en rond : j'ai l'impression qu'il me manque une donnée.
La solution
Alors je vais relire l'énoncé, voir si j'ai oublié quelque chose. Mais non, rien. OK, il est tard mais enfin quand même, ça ne peut pas être si compliqué. Alors je craque, je sais, je suis faible : je vais voir la solution. Qui tient en quelques lignes :
On trace le segment qui relie les centres des grands cercles. Alors la diagonale du rectangle obtenue est formée de deux grands rayons et deux petits rayons. Elle mesure donc 3 cm puisque le rayon du petit cercle mesure 12 cm et le rayon du grand cercle mesure 1cm.
[…]
Ensuite (je ne cite pas la solution en entier), le théorème de Pythagore conclut de façon assez directe.
Je cligne des yeux. Une fois. Deux fois. « Hein, mais pourquoi le rayon du petit cercle c'est 1/2 ?! »
Je pose la question sur le réseau social où la publication a été partagée, et une collègue me répond gentiment : « Parce que son diamètre est égal à la largeur du rectangle, qui fait 1... »
…
Ah ben oui, c'est évident en fait. Comme quoi, il ne faut rien faire après 22 h.
Et ce matin
Bon, je regarde de nouveau cet exercice, OK je suis convaincu. Donc je partage de nouveau ça à mes collègues, mais sans leur donner la solution.
Je suis rassuré : en fait, on a tous plus ou moins séché dessus. Et surtout, une question apparaît : « Mais en fait, le centre du petit cercle, est-ce vraiment le centre du rectangle ? Parce que sinon, les sommets du rectangle ne sont pas alignés avec le centre et du coup la diagonale ne mesure plus 3 cm »
Un collègue répond que c'est probablement sous-entendu dans l'énoncé, mais je n'y crois pas trop. J'ai quand même l'impression que c'est une propriété de la figure, le centre du cercle est nécessairement le centre du rectangle. On doit pouvoir démontrer ça.
Bon, il est temps de ressortir crayon à papier et feuille de brouillon. Notons $F$ le point de tangence entre le petit cercle et le segment [AB] et G le point de tangence entre le cercle et le segment [DC] :
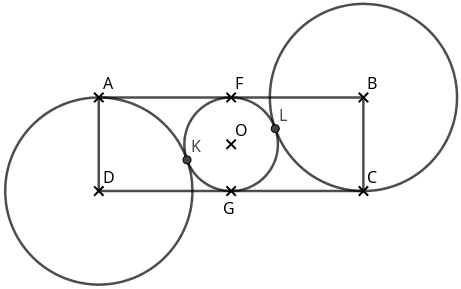
Un collègue propose que les tangentes en K et e L sont perpendiculaires à CD, mais on écarte très vite cette possibilité. Je fais une tentative avec des triangles égaux, mais ça coince : on n'arrive pas à montrer que AF=FB sans utiliser à un moment ou à un autre le fait que O est le centre. Or, c'est ce que l'ont veut démontrer.
Un autre collègue, qui depuis le début n'a pas trop pris part au débat, écrit juste un message : « On peut pas montrer que c'est le milieu de la diagonale parce que c est le milieu niveau ordonnée et un argument de symétrie ? »
Mouais, peut-être. Enfin, ça a l'air possible mais ce n'est pas ma vision des mathématiques : pour s'en convaincre, il faut le rédiger. Soit, ça m'intrigue : je creuse. De toute façon, on n'a pas d'autre idée.
Bon, déjà O est au milieu verticalement, puisque centre du petit cercle. Est-ce qu'il est au milieu horizontalement ? Si ce n'est pas le cas, disons par exemple qu'il est plus proche de [AD] que de [BC], alors cela veut dire que le cercle de centre D qui passe par A a un rayon plus petit que le cercle de centre B qui passe par C… Et ça ce n'est pas possible !
OUF ! Voilà, le point O est le centre du rectangle. Ensuite, le raisonnement vu plus haut est valide.
Les maths <3
Finalement, cette discussion nous a bien occupé pendant 1 h. Et ça fait vraiment plaisir de faire des maths, même élémentaires, de réfléchir à un problème. Comme toujours, une fois résolu, on se dit que finalement ce n'était pas si simple et qu'on a été un peu ridicules à y passer autant de temps.
Mais voilà de quoi concocter un problème vraiment sympa pour les 4e ou les 3e. À méditer…
Article court : simple retranscription d'une brève discussion avec deux élèves de 3e. Le contexte : les cours on repris lundi dans le marasme le plus total, avec un protocole sanitaire qui n'a de « renforcé » que le nom.
Alors dans un couloir, deux élèves se questionnent sur le nettoyage des bâtiments en …
SuiteCe matin, entre deux cours. Comme toujours, j'étais un peu pressé parce que la prochaine classe devait arriver et il y a toujours quelques préparatifs, en moins de 5 minutes top chrono !
Une de mes élèves, en troisième, vient me voir. C'est une élève plutôt studieuse, impliquée dans sa scolarité …
Suite